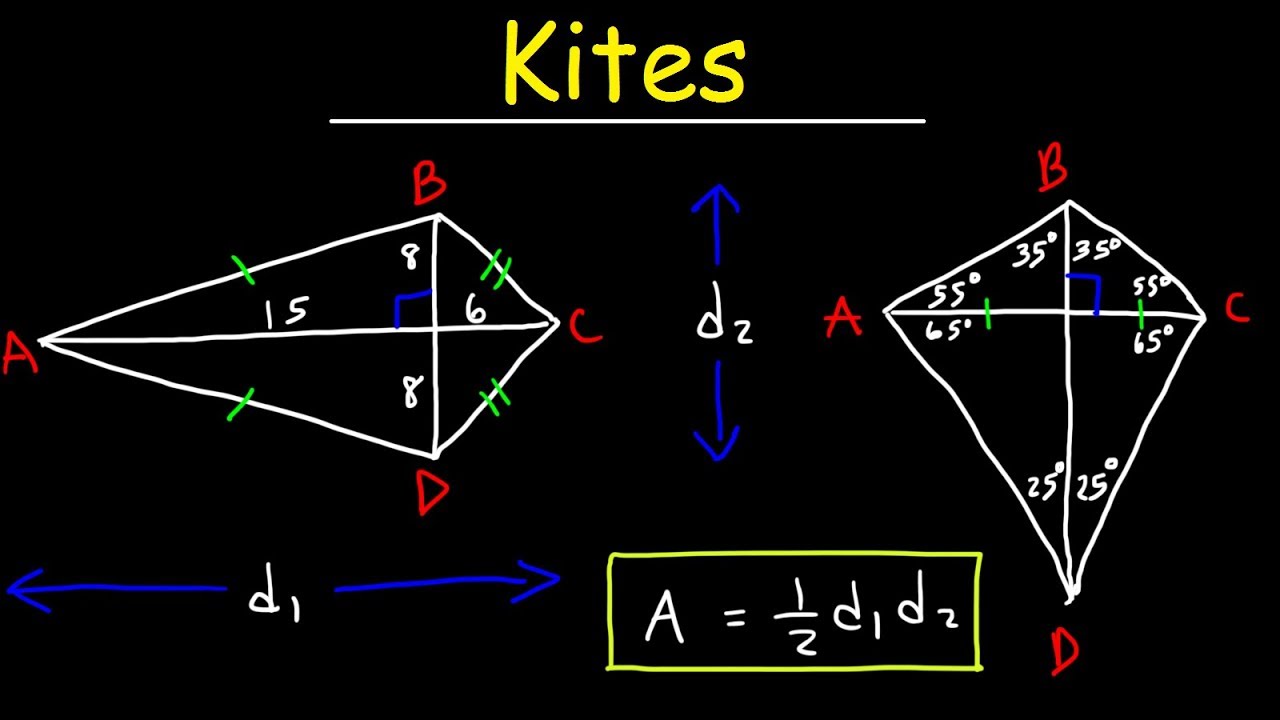
Kite Diagonals Bisect Opposite Angles . So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. The opposite angles at the endpoints of the cross diagonal are. Figure \(\pageindex{5}\) \( \delta ket\) and. $\left[\angle prs = \angle qrs, \;and\; the diagonals of a kite intersect each other at right angles. The diagonals of a kite are perpendicular. The intersection of the diagonals of a kite form 90 degree (right) angles. properties of the diagonals of a kite: This means that they are perpendicular. It can be observed that the longer diagonal bisects the shorter diagonal. the main diagonal bisects a pair of opposite angles (angle k and angle m). The angles formed at the intersection of the diagonals of a kite are congruent. This means that the two angles. the longer diagonal bisects the pair of opposite angles. the two opposite angles where the adjacent unequal sides meet are equal;
from studyschoolbartender.z21.web.core.windows.net
It can be observed that the longer diagonal bisects the shorter diagonal. properties of the diagonals of a kite: The opposite angles at the endpoints of the cross diagonal are. Figure \(\pageindex{5}\) \( \delta ket\) and. This means that they are perpendicular. the main diagonal bisects a pair of opposite angles (angle k and angle m). the longer diagonal bisects the pair of opposite angles. So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. $\left[\angle prs = \angle qrs, \;and\; This means that the two angles.
Properties Of A Kite Geometry
Kite Diagonals Bisect Opposite Angles The opposite angles at the endpoints of the cross diagonal are. It can be observed that the longer diagonal bisects the shorter diagonal. properties of the diagonals of a kite: The opposite angles at the endpoints of the cross diagonal are. Figure \(\pageindex{5}\) \( \delta ket\) and. This means that they are perpendicular. The diagonals of a kite are perpendicular. the longer diagonal bisects the pair of opposite angles. The intersection of the diagonals of a kite form 90 degree (right) angles. the two opposite angles where the adjacent unequal sides meet are equal; $\left[\angle prs = \angle qrs, \;and\; the diagonals of a kite intersect each other at right angles. This means that the two angles. So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. The angles formed at the intersection of the diagonals of a kite are congruent. the main diagonal bisects a pair of opposite angles (angle k and angle m).
From www.ck12.org
Kite Properties CK12 Foundation Kite Diagonals Bisect Opposite Angles So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. the two opposite angles where the adjacent unequal sides meet are equal; the longer diagonal bisects the pair of opposite angles. The opposite angles at the endpoints of the cross diagonal are. This means that they are perpendicular. Figure \(\pageindex{5}\) \( \delta ket\). Kite Diagonals Bisect Opposite Angles.
From www.bbc.co.uk
Properties of quadrilaterals KS3 Maths BBC Bitesize BBC Bitesize Kite Diagonals Bisect Opposite Angles the two opposite angles where the adjacent unequal sides meet are equal; It can be observed that the longer diagonal bisects the shorter diagonal. This means that they are perpendicular. This means that the two angles. The opposite angles at the endpoints of the cross diagonal are. The diagonals of a kite are perpendicular. the diagonals of a. Kite Diagonals Bisect Opposite Angles.
From dxozhbael.blob.core.windows.net
Kite Diagonals Are Equal at Dale Gillen blog Kite Diagonals Bisect Opposite Angles This means that the two angles. properties of the diagonals of a kite: The angles formed at the intersection of the diagonals of a kite are congruent. So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. This means that they are perpendicular. The intersection of the diagonals of a kite form 90 degree. Kite Diagonals Bisect Opposite Angles.
From dxowsuaul.blob.core.windows.net
In A Kite The Diagonals Bisect Each Other at Lenard Tarbox blog Kite Diagonals Bisect Opposite Angles This means that the two angles. properties of the diagonals of a kite: So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. the two opposite angles where the adjacent unequal sides meet are equal; It can be observed that the longer diagonal bisects the shorter diagonal. the longer diagonal bisects the. Kite Diagonals Bisect Opposite Angles.
From www.ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Diagonals Bisect Opposite Angles So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. The opposite angles at the endpoints of the cross diagonal are. This means that they are perpendicular. the diagonals of a kite intersect each other at right angles. The angles formed at the intersection of the diagonals of a kite are congruent. the. Kite Diagonals Bisect Opposite Angles.
From www.youtube.com
The Diagonals of a Parallelogram Bisect Each Other YouTube Kite Diagonals Bisect Opposite Angles So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. This means that they are perpendicular. This means that the two angles. the main diagonal bisects a pair of opposite angles (angle k and angle m). the diagonals of a kite intersect each other at right angles. $\left[\angle prs = \angle qrs, \;and\;. Kite Diagonals Bisect Opposite Angles.
From math.stackexchange.com
trigonometry Diagonals of a parallelogram Mathematics Stack Exchange Kite Diagonals Bisect Opposite Angles It can be observed that the longer diagonal bisects the shorter diagonal. Figure \(\pageindex{5}\) \( \delta ket\) and. $\left[\angle prs = \angle qrs, \;and\; the main diagonal bisects a pair of opposite angles (angle k and angle m). The angles formed at the intersection of the diagonals of a kite are congruent. So ∠abc = ∠cda, here ab, bc. Kite Diagonals Bisect Opposite Angles.
From dxowsuaul.blob.core.windows.net
In A Kite The Diagonals Bisect Each Other at Lenard Tarbox blog Kite Diagonals Bisect Opposite Angles the main diagonal bisects a pair of opposite angles (angle k and angle m). The opposite angles at the endpoints of the cross diagonal are. The diagonals of a kite are perpendicular. the two opposite angles where the adjacent unequal sides meet are equal; This means that the two angles. The angles formed at the intersection of the. Kite Diagonals Bisect Opposite Angles.
From www.showme.com
ShowMe bisect Kite Diagonals Bisect Opposite Angles This means that the two angles. Figure \(\pageindex{5}\) \( \delta ket\) and. So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. This means that they are perpendicular. the diagonals of a kite intersect each other at right angles. The diagonals of a kite are perpendicular. the main diagonal bisects a pair of. Kite Diagonals Bisect Opposite Angles.
From www.splashlearn.com
Properties of a Kite Definition, Diagonals, Examples, Facts Kite Diagonals Bisect Opposite Angles Figure \(\pageindex{5}\) \( \delta ket\) and. It can be observed that the longer diagonal bisects the shorter diagonal. the main diagonal bisects a pair of opposite angles (angle k and angle m). This means that they are perpendicular. The opposite angles at the endpoints of the cross diagonal are. The diagonals of a kite are perpendicular. the longer. Kite Diagonals Bisect Opposite Angles.
From goodttorials.blogspot.com
How To Find Missing Angles Of A Kite Kite Diagonals Bisect Opposite Angles the two opposite angles where the adjacent unequal sides meet are equal; Figure \(\pageindex{5}\) \( \delta ket\) and. the diagonals of a kite intersect each other at right angles. This means that the two angles. The angles formed at the intersection of the diagonals of a kite are congruent. The diagonals of a kite are perpendicular. $\left[\angle prs. Kite Diagonals Bisect Opposite Angles.
From dxozhbael.blob.core.windows.net
Kite Diagonals Are Equal at Dale Gillen blog Kite Diagonals Bisect Opposite Angles Figure \(\pageindex{5}\) \( \delta ket\) and. properties of the diagonals of a kite: the two opposite angles where the adjacent unequal sides meet are equal; The opposite angles at the endpoints of the cross diagonal are. the diagonals of a kite intersect each other at right angles. This means that the two angles. The diagonals of a. Kite Diagonals Bisect Opposite Angles.
From id.hutomosungkar.com
4+ How To Find The Area Of Kite New Hutomo Kite Diagonals Bisect Opposite Angles The intersection of the diagonals of a kite form 90 degree (right) angles. properties of the diagonals of a kite: $\left[\angle prs = \angle qrs, \;and\; The diagonals of a kite are perpendicular. the main diagonal bisects a pair of opposite angles (angle k and angle m). This means that the two angles. Figure \(\pageindex{5}\) \( \delta ket\). Kite Diagonals Bisect Opposite Angles.
From www.youtube.com
Diagonal of Rhombus bisect each other at Right Angles YouTube Kite Diagonals Bisect Opposite Angles So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. the two opposite angles where the adjacent unequal sides meet are equal; properties of the diagonals of a kite: the main diagonal bisects a pair of opposite angles (angle k and angle m). the longer diagonal bisects the pair of opposite. Kite Diagonals Bisect Opposite Angles.
From www.bartleby.com
Answered What are the properties of a Kite?… bartleby Kite Diagonals Bisect Opposite Angles This means that the two angles. The opposite angles at the endpoints of the cross diagonal are. $\left[\angle prs = \angle qrs, \;and\; the main diagonal bisects a pair of opposite angles (angle k and angle m). the longer diagonal bisects the pair of opposite angles. Figure \(\pageindex{5}\) \( \delta ket\) and. So ∠abc = ∠cda, here ab,. Kite Diagonals Bisect Opposite Angles.
From www.teachoo.com
Question 2 Show that if diagonals of a quadrilateral bisect Kite Diagonals Bisect Opposite Angles So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. The diagonals of a kite are perpendicular. the two opposite angles where the adjacent unequal sides meet are equal; The angles formed at the intersection of the diagonals of a kite are congruent. This means that the two angles. It can be observed that. Kite Diagonals Bisect Opposite Angles.
From gilitdesigner.weebly.com
gilitdesigner Blog Kite Diagonals Bisect Opposite Angles So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. the main diagonal bisects a pair of opposite angles (angle k and angle m). This means that the two angles. The angles formed at the intersection of the diagonals of a kite are congruent. The opposite angles at the endpoints of the cross diagonal. Kite Diagonals Bisect Opposite Angles.
From exopvbjbk.blob.core.windows.net
Kite Angles Diagram at Denise Piotrowski blog Kite Diagonals Bisect Opposite Angles It can be observed that the longer diagonal bisects the shorter diagonal. This means that the two angles. properties of the diagonals of a kite: So ∠abc = ∠cda, here ab, bc and cd, da are two pairs of adjacent. the two opposite angles where the adjacent unequal sides meet are equal; the longer diagonal bisects the. Kite Diagonals Bisect Opposite Angles.